邮局需要你来帮助他们为某个邮递员设计出一条能够穿过那些遥远乡村的所有村子和小鹿至少一次的邮路（输入数据将会保证这么一条路是一定存在的）。
但是，每条路线都是有一个花费的。各个村子里的村民希望邮递员到达他们村子的时间越早越好。因此，各个村子里的人们采用了一些措施：假设第 i号村子是邮递员在他的邮递路线上到达的第 k 个村子。如果 k<=w（i），那么这个村子的村民就会付给邮局 w(i)-k 欧元。当然，如果 k>w（i），邮局也同意付 w(i)-k 欧元给这个村子，对某些村子重复经过要重复收费。此外，邮递员每经过一条小路，邮局也要付给邮递员 1欧元作为补贴。
现在有n个村子，编号依次为1 到n。邮局就位于1号村子，因此邮递员的传递路线从这里开始，也从这个村子结束。能够离开每个存在的路口的数目一定是 2,4 或者 8。这里允许出现同样的村子间存在多条小路，或者某条小路构成了一个自环的情况。
你的任务是设计一个路线使得邮局赚的钱最多（或者说赔的钱最少）。如果有多重最优解，输出字典序最小的。

第 1行：两个整数 n，m，分别表示村子的数量和小路的数量；
接下来n行，每行一个整数：w(i)（1<=w(i)<1000） ；
接下来m行，每行两个整数 u、v，表示这条小路连接的村子的编号。

第 1行：一个整数k，你的程序所设计的路径的长度；
第 2 行：k+1 个整数，v1、v2、…、vk+1，每个数之间用一个空格隔开，表示你设计的路径所经过的村子的编号，其中需要满足：v1=vk+1=1。

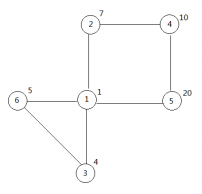
6 7
1
7
4
10
20
5
2 4
1 5
2 1
4 5
3 6
1 6
1 3

7
1 5 4 2 1 6 3 1