从玉龙雪山下来后，同学们来到了传说中的大理皇宫，看着皇宫外的平面图，大家都想知道大理皇宫到底有多少个房间？其中最大的房间有多大？由于大理皇宫非常大，同学们在雪山上玩得太累了，都点不清房间的数目了，这时聪明的小s同学想到了一个好主意，她说我们把平面图拍下来带回去让小朋友们编个程序数吧！这个主意得到了大家的一致同意，现在你的任务是帮助小s去数一数房间的数目和最大的房间的大小。而且小s在回来的飞机上还想出了一个更难的问题，她想拆掉一堵墙来制造一个更大的房间，如果你能解决这个难题，小s将会额外给你一件奖品。皇宫的平面图被分为 M(宽)*N个小正方形，每个这样的小正方形有0到4堵墙。皇宫在它的外部边缘总是有墙壁的，好用来遮挡风雨。在下面的例子中标注了一个皇宫的平面图，为了让大家能更好地理解本问题，我们用两种方法表示皇宫的平面图，第一种是用表格来表示，其中粗线表示墙壁，细线表示没有墙壁。第二种用文本表示。
┏━┯━┳━┯━┳━┯━┯━┓
1┃ │ ┃ │ ┃ │ │ ┃
┣━╅─╄━╅─╂─╆━╅─┨ Ｎ
2┃ ┃ │ ┃ ┃ ┃ ┃ ┃ ↑
┠─╄━┽─╊━╉─╊━╉─┨Ｗ←┼→Ｅ
3┃ │ │ ┃ ┃ ┃ ┃ ┃ ↓
┠─╆━┿━╃─╄━╃─╂─┨ Ｓ
4┃->┃ │ │ │ │ ┃ ┃
┗━┻━┷━┷━┷━┷━┻━┛
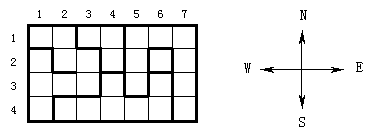
1 2 3 4 5 6 7
#############################
1 # | # | # | | #
#####---#####---#---#####---#
2 # # | # # # # #
#---#####---#####---#####---#
3 # | | # # # # #
#---#########---#####---#---#
4 # -># | | | | # #
#############################
# 表示墙壁 -,| 表示没有墙壁
->表示拆掉这堵墙后得到的新房间最大
样例中的皇宫的大小是7 x 4。
我们定义一个 “房间”是指平面图中连接在一起的中间没有墙壁隔开的“小正方形”的总体。这个平面图包含5个房间。它们的大小分别是9,7,3,1,和8。把那堵用箭头标记的墙壁拆掉后合并出的新房间将是拆掉一堵墙所能产生的最大房间，这个房间由16个小正方形组成。皇宫至少有二个房间并且总是有一堵墙壁可供拆掉。
皇宫平面图用一个二维数组来储存，每个数描述一个小正方形，共有N行数据，每行有M个数。输入顺序符合上例的编号方式。每个小正方形的墙的特征用整数P来描述（0≤P≤15）。P是下面4个可能取到的数字之和： 1: 在小正方形的西面有墙，平面图中西面即左边 2: 在小正方形的北面有墙，平面图中北面即上边 4: 在小正方形的东面有墙，平面图中东面即右边 8: 在小正方形的南面有墙，平面图中南面即下边内部的墙壁会被定义两次，小正方形(1,1)南面的墙也同时是小正方形(2,1)北面的墙。小正方形(1,1)的南面、北面和西面都有墙，所以它的特征数P=8+2+1=11。第1行有两个用空格隔开的整数M 和 N ，其中1<=M,N<=1000。第2到 N+1行: 每行M个用空格隔开的整数，表示该行小正方形的墙的特征。
40%的数据满足 1<=M,N<=50 100%的数据满足 1<=M,N<=1000