魔法学院有n（1≤n≤50）个街区，某些街区有公共汽车线路相连，如图所示，街区1和2有一条公共汽车线路相连，且由街区1至2的时间为34分钟，由街区1至街区5最快走法是1→3→5，总时间为44分钟。

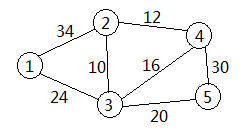
魔法学院为了改善交通，决定增加m(1≤m≤10)条公共汽车线路，若在某两街区a和b之间加开线路（前提是a和b之间必须已有线路），则从a到b的通行时间缩小为原来一半，例如，若在1和2之间加开一条线路，时间变为17分钟，若加开两条线路，时间变为8.5分钟，依次类推，所有的线路都是环线，即如果由1至2时间变为17分钟，则由2至1的时间也变为17分钟。求加开某些线路，能使由1至n的时间最少。例如，m=2，则加开1~3，3~5的线路，总时间可以减少为22分钟。求加开哪些线路，可使街区1到n的时间最短，并输出增加的线路。

第一行为街区数n和增加公共汽车线路数m。
随后的每一行三个整数x，y，d，表示x街区到y街区的通行时间d。

第一行为从街区1到街区n的最短时间。
随后m行表示增加的线路，线路需按前后顺序依次输出。

5 2
1 2 34
1 3 24
2 3 10
2 4 12
3 4 16
3 5 20
4 5 30

22
1 3
3 5