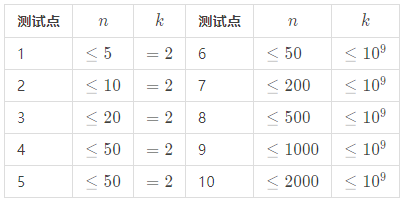
| 序号 | 标题 | 作者 | 发表时间 | 费用 | 订购数 | 操作 |
|---|
九条可怜是一个热爱出题的女孩子。
虽然出题本身是一件非常有趣的事情,但是要把题目给出成正式比赛,就不是那么有趣了:造数据总是一件让人心力憔悴的事情。
在 ZJOI2018 Day 1 中,可怜出了一道和树相关的非常有趣的题,她打算采用一种常用的方式随机生成一棵 nn 个节点的有根树:
- 节点 1 作为树的根。
- 对于 $ i \in [2, n]$ ,独立地从 $[1, i)$ 中等概率随机选取一个节点作为 $i$ 的父亲。
可怜不是很想考虑这样随机出来的数据能不能卡掉暴力,毕竟乱搞也是 OI 比赛的一部分。
可怜比较在意的是题目的区分度,以及是不是所有可能的分数都出现了。因此,可怜希望任何两个测试点的树是有区别的:这样就可能会有错误的程序能只通过其中一个点。
因此,可怜想要计算,通过上面的方法独立的随机生成 kk 棵 nn 个节点的有根树 $T_1$ 至 $T_k$ ,他们两两同构的概率是多少。
两棵 $n$ 个节点的有根树 $T_1$ 和 $T_2$ 同构当且仅当存在长度为 nn 的排列 pp,满足 $p_1 = 1$ ,且对于 $ \forall i \in [2, n]$,若 $i$ 在 $T_1$ 的父亲是 $f$ ,则 $p_i$ 在 $T_2$ 的父亲是 $p_f$ 。