题目描述
某市正在举行一场大型博览会,博览会有 n 个展馆,每个展馆里有若干个展台。
这 n 个展馆以及它们之间的道路可以看成一棵二叉树,博览会的出入口设在根节点—— 1 号展馆,小明将从这里出发乘坐电瓶车到各个展馆参观,并最终回到 1 号展馆出口。
由于路程差异,乘坐电瓶车往返不同展馆间的费用也有所区别。
出发时,小明的乘车卡里余额为 k。他现在想知道,若全程都乘坐电瓶车,他最多能参观多少个展台?
输入
输入共 n + 2 行:
第 1 行为 2 个整数 n , k,用一个空格隔开,表示展馆个数和小明乘车卡初始余额。
第 2 行为 n 个数,用一个空格隔开,表示 1 号至 n 号各展馆的展台数目。
接下来 n 行,每行 4 个数,用一个空格隔开;
第 i + 2 行 4 个数分别表示展馆i左子节点展馆号、到左子节点展馆的费用、右子节点展馆号、到右子节点展馆的费用。
如果子节点展馆号为 0 则表示没有对应的子节点展馆。
输出
输出共 1 行, 1 个整数,表示小明最多能参观的展台数量。
样例输入输出
输入#1
复制
10 20
2 8 5 1 10 5 9 9 3 5
2 1 3 2
4 8 5 2
6 2 7 2
8 3 9 6
0 0 10 2
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
提示
根据样例数据,可以得到如下展馆二叉树示意图(每个圈内标示了展馆号及展台数):
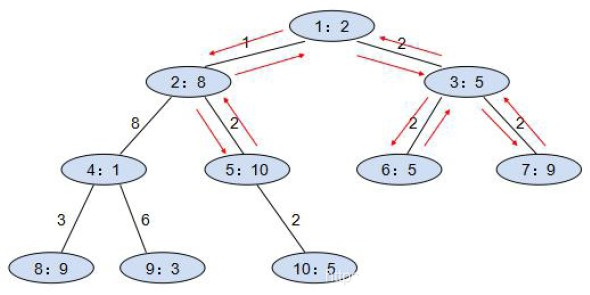
由图可知,小明沿红色箭号路径,到1、2、5、3、6、7这六个展馆参观并返回,往返乘车费用为18,参观展台数为39,为能够实现的最大值。