乐乐做了个梦，梦见自己当了国王。乐乐王国有N座城市（编号从1~N，首都的编号为1）。乐乐王国的道路构成树状结构：首都1与几个大城市相连，这几个大城市又通过道路与一些稍小的城市相连……严格地说，这N座城市构成一棵有根树（1为树根），城市i的管理区域为以i为根的子树。
道路都是双向的。经过每条道路需要收费，从城市A到城市B的花费为A到B的简单路径上所有道路的费用之和（不妨称之为城市对(A, B)之间的花费）。显然，一棵树上任意两点之间的简单路径（即不能重复经过某个点的路径）是唯一的。
由于物价飞涨，经过一番缜密的思考，乐乐决定重新规划自己国家的道路收费。具体来说，他要进行Q个操作，每个操作是如下两种类型：
INC u v w 
——表示u到v的路径上，所有的道路的收费增加w；
ASK p
——表示询问城市p的管理区域中，所有的“城市对”的花费之和。比如，城市p的管理区域（即以p为根子树）中有城市c1, c2, c3, …，cs（这里面包括p），询问所有的城市对(c1, c2), (c1, c3), …, (c2, c3), …,(cs-1, cs)的花费之和。
乐乐把这个问题交给你，快帮帮他吧！

第一行输入两个正整数N，Q，分别表示城市的数目和操作的数目。
接下来有N – 1行，第i行是两个正整数p[i], c[i]，表示城市p[i]是城市i的父亲结点，且连接p[i]和i的道路的初始收费为c[i]（1≤c[i]≤1000）。
接下来有Q行，每行是如下两种类型之一：
INC u v w (u, v, w都是整数，且1≤u, v≤N, 0≤w≤1000，注意u, v可能相等)
ASK p   (p是整数，且0≤p≤1000)
意义如题目所述。

对每个ASK类型的操作，输出所求的答案。请你输出答案对2018取模后的结果。

5 5
1 1
2 5
1 2
2 1
INC 2 4 2
INC 3 4 1
ASK 2
INC 2 5 3
ASK 1

14
84

【样例解释】
乐乐王国的地图如下：
   
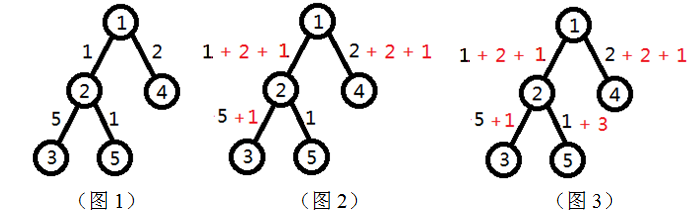
如图1，城市1的管理区域是1,2,3,4,5；城市2的管理区域是2,3,5；城市3,4,5的管理区域是它们自己。
经过前两次操作，道路费用变化如图2。
这时，(2, 3), (2, 5), (3, 5)的费用和 = 6 + 1 + 7 = 14。
再进行一次修改（第4个操作），变化如图3。
这时，(1,2)(1,3)(1,4)(1,5)(2,3)(2,4)(2,5)(3,4)(3,5)(4,5)的总费用为：
4+10+5+8+6+9+4+15+10+13=84
约定
对于20%的数据，1≤Q, N≤200；
对于40%的数据，1≤Q, N≤5,000;
对于70%的数据，1≤Q, N≤50,000，且树的深度（即每个城市到首都经过的道路数目最大值）不会太大；
对于100%的数据，1≤Q, N≤50,000，树的深度不超过10000，其他输入数据的范围在输入格式中已给出。