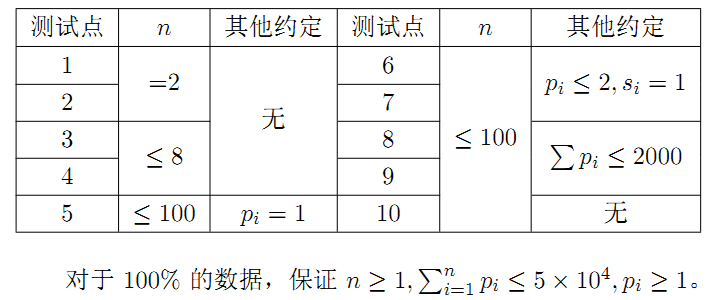
| 序号 | 标题 | 作者 | 发表时间 | 费用 | 订购数 | 操作 |
|---|
九条可怜是一个贪玩的女孩子。
这天,她和她的好朋友法海哥哥去玩密室逃脱。在他们面前的是$n$个开关,开始每个开关都是关闭的状态。要通过这关,必须要让开关达到指定的状态。目标状态由一个长度为$n$的$01$
数组$s$给出,$si=0$表示第$i$个开关在最后需要是关着的,$si=1$表示第$i$个开关在最后需要被打开。
然而作为闯关者,可怜和法海并不知道$s$。因此他们决定采用一个比较稳妥的方法:瞎按。他们根据开关的外形、位置,通过一些玄学的方法给每一个开关赋予了一个权值$p_i(p_i>0)$每一次,他们会以正比于$p_i$的概率(第$i$个开关被选中的概率是$\frac{p_i}{\sum^n_{j=1}p_j}$选择并按下一个开关。开关被按下后,状态会被反转,即开变关,关变开。注意,每一轮的选择都是完全独立的。
在按开关的过程中,一旦当前开关的状态达到了$s$那么可怜和法海面前的门就会打开,他们会马上停止按开关的过程并前往下一关。作为一名欧皇,可怜在按了$\sum^n_{i=1}s_i$次后,就打开了大门。为了感受一下自己的运气是多么的好,可怜想要让你帮她计算一下,用这种随机按的方式,期望需要按多少次开关才能通过这一关。