经过多日来的努力，jakrinchose制作出一部CDMA移动电话(！)，随即拨通了正在出航的ZSU号上的卫星电话.ZSU号马上调转航向前往神秘岛。
十日后的傍晚，ZSU号来到神秘岛海域的外则，正在专心掌陀的dynamic忽然收到在船顶监视海面状况的gpy的紧急呼叫“前方海域有异常，暂停前进！暂停前进！”而在雷达前监测的inkfish却摇摇头，表示并没发现异常状况，但为了小心起见，dynamic还是马上停航！当大家用望远镜观察时，发现前方远处的一片海域中，隐现一团漆黑，光线完全透不过，因此决定等到第二天再走近一点观察清楚。
第二日，由ljy和Savior驾驶一辆快艇，前往观察这团异物，当尚有一段路程时，快艇就被吸了进去，当他们从这团异物中出来时，发现来到另一处陌生的海域！这团异物是一个空间传送装置！似乎是不明智慧生物布置下的防卫设施，ZSU号马上联络了Z4，要他们在岛上找出能使船驶进神秘岛的方法。jakrinchose忽然联想起了在木屋中的一块形似石板的东西，果然，石板就是控制这个海上防御的中枢！ 
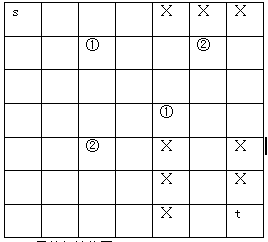
石板是一块正方形，控制着神秘岛海域上的防御布置，与之相对应，海域也是正方形，被等分成n*n格，每一格海域都在石板上有相应的一格对应，这些小格有三种：
一种表示普通海域，在该格对应的海域上船能自由航行；
一种表示礁石，船不能走进该格对应的海域；
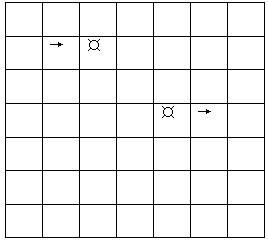
还有一种就是有若干个不同颜色的石块，每种颜色分别有两格，对应该海域上是一组空间传送装置，每一组的两个装置之间互相传送。当船正对该海域（必须要正向）驶进该海域相邻的一格海域时，船会马上被吸进空间传送装置，转移至同颜色的另一格传送装置，并沿原方向再走一格，当然这一格必须是船能够行走的，并且当ZSU从一个传送器出来后不能180度转向。举个例子，如图，箭头是ZSU号行进的方向，"¤"表示一组传送装置。（2，3）和（4，5）是同颜色的一组空间传送装置，当ZSU号从（2，1）走进（2，2）时,会马上被吸进转换装置传送至（4，5）并立即走至（4，6）。当然假如ZSU号从（1，2）走进（2，2）时，由于船的方向并没有正对转换装置，将不会发生传送。  

特别地，Z4还发现石板上某一些格子是活动的，也就是表示这些格子抽离后可以自由再组合，这样就能够局部改变神秘岛海上防御的布局。但是，前提是所有的格子都必须要放到石板上。并且为了避免出现时空混乱，任意相邻的两格不能同时是传送装置。所以Z4把所有的活格都拆了出来，想找出一种砌拼的方法方便ZSU号驶进。
jakrinchose立即提议用老规矩“猜十次”选出一人负责引导ZSU号驶进神秘岛。但立方以该责任非同小可，提出应由”猜十次”的发明者担负，随即得到除了jakrinchose外所有人的强烈赞同。
无奈的jakrinchose想知道，是否有一种石板的砌拼方法使得ZSU号能成功抵达神秘岛，且最快需要多长时间。
虽则神秘岛外海域非常广阔，但是ZSU有非常良好的性能。调转一次航向，及每移动一格，需的时间都为1。由于初始是静止在海面上的，以第一步的航向是任意的。由于传装置中是超越时空的,所以在传送过程中所需的时间为0，就是上面所提到的例子，ZSU号从（2，1）走到（2，2）用时为1，然后再从（2，2）传送到（4，6）这过程是不需要时间，所以总耗时为1！
理所当然，ZSU号不能跑出神秘岛的海域!

输入文件escape.in第一行为三个整数n,m,p,q(n<=100,m<=20,p<n*n)，n表示防御系统的范围,也对应石板的大小，m表示传送装置的组数，p表示礁石的数量。
接下来m行，每行四个整数x1,y1,x2,y2分别表示该组两个传送装置的坐标，如果坐标为（0，0）表示控制该传送装置是活格。
接下来p行，每行两个整数x,y表示该礁石的坐标，同样，（0，0）表示该控制该礁石是一个活格。
然后n行，每行n个数， 描述该石板的初始布局，第i行j列表示坐标为(i,j)的海域(or石板)， 0表示该格上是活格，1则表示非活格。
当然我们可以肯定的是，石板上放置活格的位置肯定大于或等于传送装置和礁石的活格之和，并且不排除，某些普通海域也是活格。同时，似乎为了避免不必要的混乱，在设计的时候，同一组传送装置最多只有一格是活格。最多情况下，也仅有12活格并且当中最多仅有6个传送器。
最后一行四个整数x_ZSU,y_ZUS,x_island,y_island分别是ZSU号初始位置和神秘岛的位置(肯定不会在活格中)。

输出文件escape.out只有一行,假如ZSU号不能抵达神秘岛,则输出”No solution.”,否则输出抵达神秘岛的最短时间.

7 2 10
2 3 0 0
2 6 5 3
1 5
1 6
1 7
2 4
6 5
2 5
5 5
7 5
5 7
6 7
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 0 1 1
1 1 1 1 1 1 1
1 1 1 1 1 0 1
1 1 1 1 1 1 1
1 1
7 7

9