小简单正在学习离散数学，今天的内容是图论基础，在课上他做了如下两条笔记：

一个大小为 n 的树由 n 个结点与 n − 1条无向边构成，且满足任意两个结点间有且仅有一条简单路径。在树中删去一个结点及与它关联的边，树将分裂为若干个子树；而在树中删去一条边（保留关联结点，下同），树将分裂为恰好两个子树。
对于一个大小为 n 的树与任意一个树中结点 c，称 c 是该树的重心当且仅当在树中删去 c 及与它关联的边后，分裂出的所有子树的大小均不超过 $ \lfloor \frac{n}{2} \rfloor $ （其中 $ \lfloor x \rfloor $ 是下取整函数）。对于包含至少一个结点的树，它的重心只可能有 1 或 2 个。
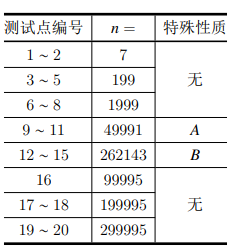
课后老师给出了一个大小为 n 的树 S，树中结点从 1 ~ n 编号。小简单的课后作业是求出 S 单独删去每条边后，分裂出的两个子树的重心编号和之和。即：
$ \sum_{(u,v) \in E} \left( \sum_{1 \leq x \leq n \atop 且 x 号点是 S'_u 的重心} x + \sum_{1 \leq y \leq n \atop 且 y 号点是 S'_v 的重心} y \right) $
上式中，E 表示树 S 的边集，(u,v) 表示一条连接 u 号点和 v 号点的边。$ S'_u  与 S'_v $  分别表示树 S 删去边 (u,v) 后，u号点与 v号点所在的被分裂出的子树。

小简单觉得作业并不简单，只好向你求助，请你教教他。

本题包含多组测试数据
第一行一个整数 T 表示数据组数。
接下来依次给出每组输入数据，对于每组数据：
第一行一个整数 n 表示树 S 的大小。
接下来 n − 1 行，每行两个以空格分隔的整数 ui, vi，表示树中的一条边 (ui, vi)。

共 T 行，每行一个整数，第 i 行的整数表示：第 i 组数据给出的树单独删去每条边后，分裂出的两个子树的重心编号和之和。

2
5
1 2
2 3
2 4
3 5
7
1 2
1 3
1 4
3 5
3 6
6 7

32
56