给定一个长度为 $n$ 的正整数序列 $a_i$,下标从 $1$ 开始编号。我们将该序列视为一个首尾相邻的环,更具体地,对于下标为 $i$,$j$ $(i \le j)$ 的两个数 $a_i , a_j$,它们的距离为 $min ( j - i , i + n - j )$。
现在再给定 $m$ 个整数 $k_1 , k_2 , \ldots , k_m$,对每个 $k_i$ $( i = 1 , 2 , \ldots , m)$,你需要将上面的序列 $a_i$ 重新排列,使得环上任意两个距离为 $k_i$ 的数字的乘积之和最大。
【样例1解释】
$k_i = 0$ 时:答案为每个数平方的和。
$k_i = 1$ 时:一种最优方案:$\{3,1,2,4,6,5\}$,答案为:
$$3 × 1 + 1 × 2 + 2 × 4 + 4 × 6 + 6 × 5 + 5 × 3 = 82$$
$k_i = 2$ 时:一种最优方案:$\{3,6,1,4,2,5\}$,答案为:
$$3 × 1 + 1 × 2 + 2 × 3 + 6 × 4 + 4 × 5 + 5 × 6 = 85$$
【数据范围与提示】
对于所有测试数据:$1 \le m \le n \le 2 \times 10^5,0 \le k \le \lfloor \frac{n}{2}\rfloor ,1 \le a_i \le 10^5$。
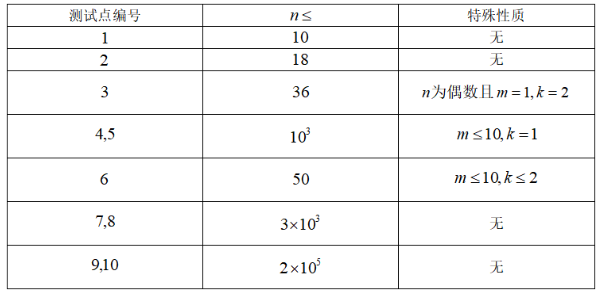
每个测试点的具体限制见下表: