题目描述
你有 $10^{20}$ 个格子,它们从 0 开始编号,初始时所有格子都还未染色,现在你按如下规则对它们染色:
1. 编号是 $p_1$ 倍数的格子(包括 0 号格子,下同)染成红色。
2. 编号是 $p_2$ 倍数的格子染成蓝色。
3. 编号既是 $p_1$ 倍数又是 $p_2$ 倍数的格子,你可以选择染成红色或者蓝色。
其中$p_1$ 和 $p_2$ 是给定的整数,若格子编号是 $p_1$ 或 $p_2$ 的倍数则它必须要被染色。在忽略掉所有未染色格子后,你不希望存在 $k$ 个连续的格子颜色相同,因为你认为这种染色方案是无聊的。现在给定 $p_2, p_2, k$,你想知道是否有一种染色方案不是无聊的。
输入
本题包含多组数据。
第一行一个整数 T 表示数据组数。
每组数据一行三个正整数 $p_2, p_2, k$ ,变量意义见题目描述。
输出
对于每组数据,输出一行一个字符串,若存在一种染色方案不是无聊的,则输出 "Yes"(不含引号,下同),否则输出 "No"。
样例输入输出
输入#1
复制
4
2 10 4
2 3 6
1 4 7
1 1 2
输入#2
复制
8
370359350 416913505 3
761592061 153246036 6
262185277 924417743 5
668232501 586472717 2
891054824 169842323 6
629603359 397927152 2
2614104 175031972 68
924509243 421614240 4
输出#2
复制
Yes
Yes
Yes
No
No
No
Yes
Yes
提示
【数据范围】 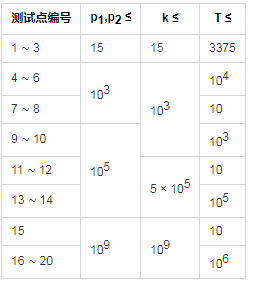
对于所有测试点:$1\leq T\leq 10^6 ,1\leq p_1,p_2,k\le 10^9 $。
