时隔数年，刺客荆轲再次来到咸阳宫，试图刺杀嬴政。

咸阳宫的地图可以描述为一个 n 行 m 列的矩形。在这里，我们规定每一行中从左到右为 x 轴正方向，每一列中从下到上为 y 轴正方向，左下角的点坐标为 (1,1)。矩形中的点可以分为 4 种：

1. 起点，也就是荆轲的所在点，在地图中用字符"S"代表。
2. 终点，也就是嬴政的所在点，在地图中用字符"T"代表。
3. 卫兵，在地图中用一个正整数 $a_{i,j}$ 代表。在这里，一个卫兵 $(i,j)$ 可以观察到与他曼哈顿距离小于 $a_{i,j}$   的点。也就是卫兵 $(i,j)$ 可以观察到所有满足 $|x-i|+|y-j|<a_{i,j}$ 的点 $(x,y)$。
4. 空地，在地图中用字符"."代表。

荆轲的正常移动方式为每秒向八连通的任意方向前进一格。如下图，中间的点为荆轲当前所在点，每一秒，他可以走向其余的八个点。


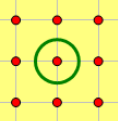
需要注意的是，正常移动时，荆轲不能踏进任何一个有卫兵或者卫兵能观察到的格子。当然，他也不能走出咸阳宫，也就是说，无论何时，荆轲的坐标 $(x,y)$ 都必须满足 $1\le x\le m$ 且 $1\le y\le n$。

荆轲还有两种技能：隐身和瞬移。

1. 隐身：下一秒荆轲进入隐身状态，卫兵观察不到荆轲，荆轲可以进入卫兵的观察范围内，但仍然不能进入卫兵所在的格子。注意这个状态只能维持一秒。
2. 瞬移：荆轲下一秒移动的距离改为 $d$，但这时只能向上下左右四个方向移动。即可以移动到 $(x+d,y)，(x-d,y)，(x,d+y)，(x,d-y)$。
在本题中，两种技能可以同时使用，而且不考虑冷却时间，即一次用完可以立即用下一次，两种技能都分别有使用次数限制，你也可以不用完所有次数。

现在给出咸阳城的地图，请计算荆轲到达秦王所在点所需的最短时间。此外，在所用时间相同情况下，荆轲希望使用的两种技能总次数尽可能少；在所用时间与技能次数相同情况下，荆轲希望使用的隐身次数尽可能少。

第一行五个整数 $n,m,c_1,c_2,d$，代表地图的大小为 $n\times m$，隐身的使用限制次数为 $c_1$，瞬移的使用限制次数为 $c_2$  和一次瞬移的距离为 d。

接下来 $n$ 行，每行 $m$ 个元素。每个元素为字符‘S’、‘T’、‘.’$或者一个正整数 $a_{i,j}$ ，代表一个格点，具体含义详见题目描述。

若荆轲无法到达秦王所在点，则输出一行一个 -1。
否则输出一行三个整数 $t,u_1,u_2$ ，依次代表所需的最短时间，隐身的使用次数与瞬移的使用次数。

5 4 0 0 5
. 1 T 1
. . . 2
. 1 . .
S . . .
1 . . .

3 0 0

8 6 2 3 3
. S . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
2 . 2 . 2 .
. . 1 . T .
3 . 1 . . 3

3 1 3

8 6 5 5 2
. S . . . .
. . . . . .
. . . . . .
1 1 3 2 . 1
2 3 2 2 1 3 
3 2 4 1 4 3 
2 6 1 5 T 2 
8 1 6 3 2 10

-1