【样例解释】
第 $1$ 次操作时，将 $1$ 所在树的根 $1$ 接在 $0$ 所在树的根 $0$ 下。    
第 $2$ 次操作时，将 $2$ 所在树的根 $2$ 接在 $0$ 所在树的根 $0$ 下。  
第 $3$ 次操作时，$1$ 所在树如图 $1$，在 $0,1,2$ 中分别填入 $[0,1,2]$ 和 $[0,2,1]$ 可以产生 $2$ 种不同的堆。    
第 $4$ 次操作时 $x=(3+2) \mod 5=0 ,y=(1+2) \mod 5=3$，将 $0$ 所在树的根 $0$ 接在 $3$ 所在树的根 $3$ 下。  
第 $5$ 次操作 时，$x=(2+2) \mod 5=4 ,y=(0+2) \mod 5=2$，将 $4$ 所在树的根 $4$ 接在 $2$ 所在树的根 $3$ 下。    
第 $6$ 次操作 时，$x=(4+2) \mod 5=1$，$1$ 所在树如图 $2$，在 $0\sim 4$ 中分别填入 $[1,2,3,0,4],[1,3,2,0,4],[1,2,4,0,3],[1,4,2,0,3],[1,3,4,0,2],[1,4,3,0,2],[2,4,3,0,1]$ 可以产生 $8$ 种不同的堆。

【数据规模与约定】 对于 $100\%$ 的数据， $0\le x',y' <n \le 3\times 10^5 ,1\le Q\le 3\times 10^5$。
对于不同测试点，我们约定：

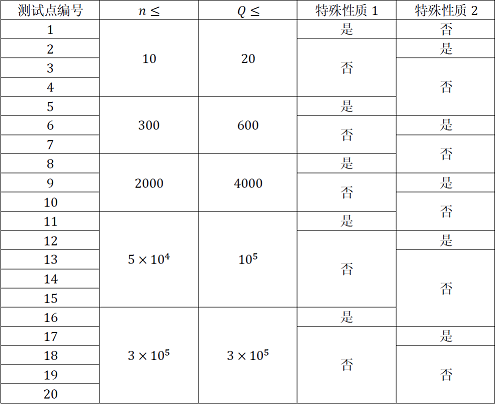
特殊性质 $1$：存在 $1≤i<n$，前 $i$ 次操作均为 $1$ 操作，之后全是 $2$ 操作。
特殊性质 $2$：对于所有输入 $x$ 和 $y$ 本身即是其所在树的根。