题目描述
给定一个 $2\times n$ 的长方形网格,请从中找出一片凸型的区域,使得这片区域的分数之和达到最大。以下是一个例子,黑框表示分数最大的凸型区域:
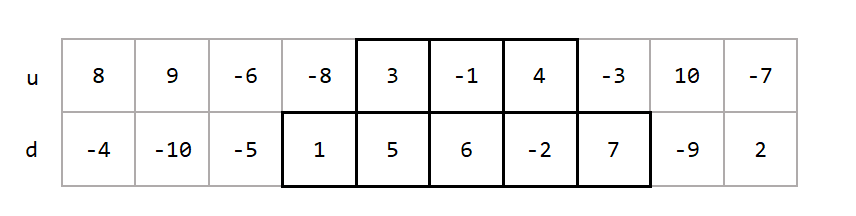
给定 $u_1,u_2,\cdots,u_n$ 以及 $d_1,d_2,\cdots,d_n$,请找到四个下标满足
$$1\leq i
输入
第一行:单个正整数表示 $n$。
第二行:$n$ 个整数表示 $u_1,u_2,\cdots,u_n$。
第三行:$n$ 个整数表示 $d_1,d_2,\cdots,d_n$。
输出
单个整数:表示凸型区域的最大分数之和。
样例输入输出
输入#1
复制
10
8 9 -6 -8 3 -1 4 -3 10 -7
-4 -10 -5 1 5 6 -2 7 -9 2
提示
+ 对于 $25\%$ 的分数, $5\leq n \leq 100$;
+ 对于 $50\%$ 的分数, $5\leq n \leq 1000$;
+ 对于 $75\%$ 的分数, $5\leq n \leq 10000$;
+ 对于 $100\%$ 的分数, $5\leq n \leq 100000$;
+ $-10^4\leq u_i \leq 10^4$;
+ $-10^4\leq d_i \leq 10^4$。