题目描述
小爱有很多 $2 \times 2$ 的积木拼块,现在她打算在一个 $n \times m$ 的底板上,铺上数量若干的积木拼块,拼块之间不能重合。底板上可能已经存在一些拼块,具体位置由输入给定。请统计小爱有多少种放置拼块的方法。
举例来说,假设在一个 $3 \times 4$ 的蓝色底板上,已经存在一个拼块(以红色表示):
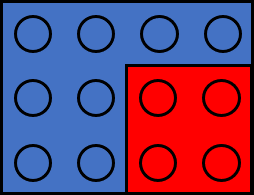
那么继续放置只有三种可能:

第一种是不放置新的拼块,第二、第三种可能方案是在绿色部分放置一块拼块。由于底板的大小有限,没有办法放置更多的拼块。
输入
第一行:三个正整数 $n$,$m$ 与 $k$;
接下来 $k$ 行,每行两个整数 $x_i$ 与 $y_i$,表示一个已经存在的拼块,$(x_i,y_i)$ 表示该拼块的左上角位置。
输出
单个整数:表示放置拼块的方案数。
样例输入输出
提示
+ $1 \leq n,m \leq 8$,$0 \leq k \leq 16$
样例1说明:即题干中的例子