题目描述
【题目背景】
待天以困之,用人以诱之,往蹇来返。
33DAI 承包了一座“满二叉树”山,山上一共有 $2^m-1$ 个山洞,山洞编号从 $1\sim 2^m-1$。
33DAI 在山上养了 $n$ 只老虎,已知第 $i$ 只老虎目前在编号为 $a_i$ 的山洞里。
山洞之间有道路相连,每条道路连接两个山洞,老虎可以在一秒钟之内通过道路从其中一个山洞转移到另一个山洞。山洞和道路都无限大,道路可以同时容纳无限老虎通行,山洞也可以容纳无限老虎。编号为 $i$ 的山洞会和编号 $\lfloor\frac{i}{2}\rfloor,\ i*2,\ i*2+1$ 的山洞之间各有一条道路(如果编号不在 $1\sim 2^m-1$ 之内则没有那个山洞也没有那条道路)。
现在 33DAI 想把所有老虎调到编号为 $2^m-1$ 的山洞中,每只老虎都会沿着最快的路径抵达,请你算算最晚到达的老虎需要多长时间能到达。
输入
第一行两个数 $n,m$。
第二行为 $n$ 个整数:$a_1\sim a_n$。
输出
一个数,即最晚到达的老虎多长时间能到达。
样例输入输出
提示
【样例1解释】
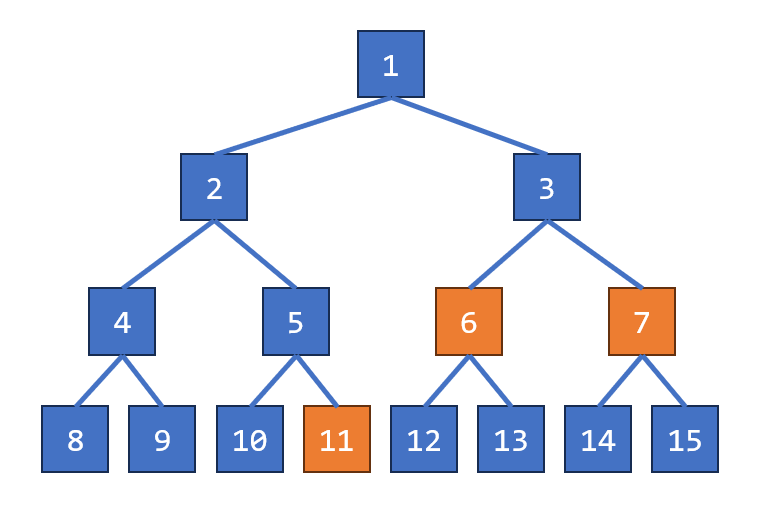
如上图,$11$ 号山洞的老虎距离 $2^4-1=15$ 号山洞最远,要花 $6$ 分钟。
【样例3解释】
$2$ 和 $13$ 到 $15$ 都需要 $4$ 分钟。
【数据规模与约定】
对于 $100\%$ 的数据,$1 \le n \le 10^5$,$1\le m\le 63$,$1\le a_i\le 2^m-1$。
- 子任务 1(10 分):保证 $n=1$。
- 子任务 2(20 分):保证 $a_i + 1$ 是某个 $2$ 的整数次幂,即存在 $x$ 使得 $a_i+1=2^x$。
- 子任务 3(30 分):保证 $m=20$。
- 子任务 4(40 分):没有特殊限制。