题目描述
【题目背景】
假之以便,唆之使前,断其援应,陷之死地。遇毒,位不当也。
33DAI 拿到了一棵 $n$ ($n\ge 2$)个节点的树,节点编号从 $1\sim n$,根节点为 $1$ 号节点。
树上的 $n-1$ 条边各有一个权值,第 $i$ 条边连接了 $u_i$ 与 $v_i$,权值为 $w_i$,表示去掉这条边需要花费 $w_i$ 元钱。
33DAI 在树之外又添加了一个超级点,超级点的编号为 $0$,超级点和每个叶子节点之间都连了一条超级边,超级边不能被去掉。
显然初始节点 $0$ 与节点 $1$ 连通。你需要把他们断开连接,请问最少需要花多少元钱。
输入
第一行一个数 $n$。
接下来 $n-1$ 行,第 $i$ 行为空格隔开的 $u_i,v_i,w_i$。
输出
一个整数,即最少需要花这么多元钱。
样例输入输出
输入#1
复制
7
1 2 100
1 3 100
4 3 30
7 4 20
3 6 30
5 3 40
输入#2
复制
7
1 2 100
1 3 100
4 3 100
7 4 100
3 6 100
5 3 100
提示
【样例1解释】
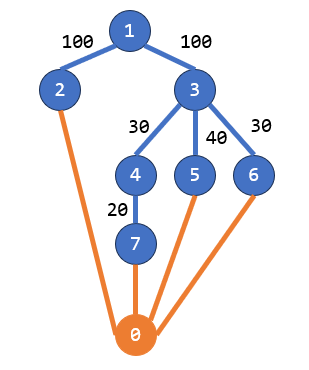
树的形态如上,显然最低花费为去掉 `1~2`、`4~7`、`3~5`、`3~6` 四条边,共花费 $100+20+40+30=190$ 元。
【样例2解释】
树的形态和上面一样,只不过边权都是 $100$ 了。
【 数据规模与约定】
对于 $100\%$ 的数据,$1 \le n,u_i,v_i,w_i \le 5000$,保证输入的构成了一棵树。
- 子任务 1(10 分):保证 $n=2$
- 子任务 2(20 分):保证只有一个叶子节点。
- 子任务 3(30 分):保证所有边权都相等。
- 子任务 4(40 分):没有特殊限制。