题目描述
小X学校的教学楼是一栋H层的建筑。学生在同一楼层间可以自由移动,但是只有通过爬楼梯才可以上下楼层。
让我们把教学楼抽象成一个有H×M个格子的矩形,学生可以从一个单元格上花费1秒移动到上下左右的相邻单元格上。学生在水平方向上的移动是没有限制的(除了不能摔出楼外),但只有在有楼梯相连的时候才能进行竖直移动。一个楼梯会连接同一列中的一段连续楼层,且一列中只会有一个楼梯。对于这一部分叙述可以通过样例理解。
现在有T个学生,每个人都希望从一个位置走到另一个位置上。他们想问问小X最短需要花费多长时间。
输入
第一行,2个整数H和M表示教学楼大小。
第二行,1个整数K表示楼梯的数量。
接下来K行,每行三个整数x,h1,h2表示在第x列的h1层和h2层之间有楼梯。
接下来1行,一个整数T表示有T个学生。
接下来T行,每行四个整数sx,sy,tx,ty表示这个学生想要从sx列的sy层走到tx列的ty 层。
输出
对于每一个学生按顺序输出一行一个整数表示最短时间。
如果不可能走到,输出-1。
样例输入输出
输入#1
复制
9 8
2
3 5 8
6 2 5
3
6 8 5 7
4 6 7 2
1 9 8 1
提示
【样例解释】
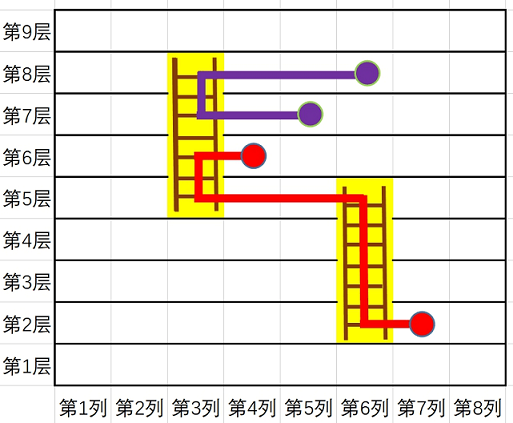
【数据范围】
本题共有15个测试点。
- 对于全部测试点:$1 \le x \le M$ 且所有$x$各不相同,$1 \le h1 \lt h2 \le H$ 对于全部测试点:$1 \le sx,tx \le M$,$1 \le sy,ty \le H$
- 对于全部测试点:$1 \le H,M \le 10^5$,$ 1 \le K \le 300$,$1 \le T \le 50000$
对于编号为奇数的测试点:T=1
- 对于测试点1-2:K=0
- 对于测试点3-4:K=1
- 对于测试点5-6:H=M=10
- 对于测试点7-10:H=M=50
- 对于测试点11-15:没有特殊限制